ДСР 4 Геометрія = ДСР 8 Математика
Бісектриса кута при основі рівнобедреного трикутника дорівнює основі цього трикутника. Знайдіть кут при основі цього трикутника.
A. 60°
Б. 72°
В. 84°
Г. 96°
Розв'язок:
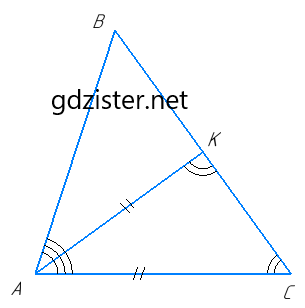
Нехай в ∆ABC AB = BC, AK — бісектриса, ∠KAC = $\frac{1}{2}$ ∠BAC.
Нехай ∠KAC = x, тоді ∠A = 2x, ∠C = ∠A = 2x (як кути при основі рівнобедреного трикутника). Оскільки AK = AC, то ∆KAC — рівнобедрений з основою KC. ∠K = ∠C (як кути при основі рівнобедреного трикутника), ∠K = 2x.
За властивістю суми кутів трикутника маємо:
x + 2x + 2x = 180°; 5x = 180°; x = 36°.
Отже, ∠A = ∠C = 36° × 2 = 72°.
Відповідь:
Б) 72°
