Завдання № 540

№ 540 Геометрія = № 41.15 Математика

Умова:

Доведіть, що два прямокутних трикутники між собою рівні, якщо висота, проведена до гіпотенузи, і катет одного трикутника дорівнюють відповідно висоті, проведеній до гіпотенузи, і катету другого трикутника.

Розв'язок:

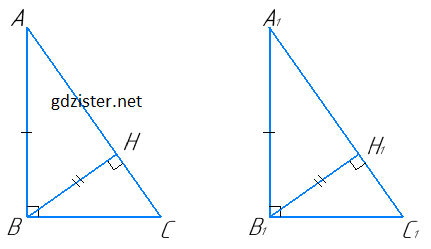
Нехай ∆ABC і ∆A₁B₁C₁ - прямокутні.
AB = A₁B₁, BH ⊥ AC, B₁H₁ ⊥ A₁C₁, BH = B₁H₁.
∆ABH = ∆A₁B₁H₁ (за катетом і гіпотенузою: AB = A₁B₁, BH = B₁H₁), тоді ∠A = ∠A₁.
∆ABC = ∆A₁B₁C₁ (за катетом і гострим кутом: AB = A₁B₁, ∠A = ∠A₁).

Відповідь: