№ 505 Геометрія = № 40.12 Математика
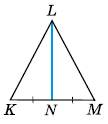
На малюнку KLM — рівнобедрений трикутник з основою KM, LN — його медіана. Знайдіть кути трикутника KLM, якщо ∠KLN = 31°.
Розв'язок:
Нехай ΔKLM — рівнобедрений, LK = LM. Оскільки LN — медіана рівнобедреного трикутника, то LN — бісектриса і висота ΔKLM. ∠KLM = 2∠KLN = 2 × 31° = 62°.
Оскільки сума кутів трикутника дорівнює 180°, то
∠K + ∠M + ∠L = 180°,
∠K + ∠M = 180° – ∠L = 180° – 62° = 118°.
∠K = ∠M як кути в основі рівнобедреного трикутника.
∠K = ∠M = 118° : 2 = 59°.
Відповідь:
62°, 59°, 59°.
