№ 411 Геометрія = № 31.13 Математика
Усередині рівнобедреного трикутника DMN (DM - DN) взято точку Р так, що МР = PN. Доведіть, що пряма DP ділить навпіл сторону MN.
Розв'язок:
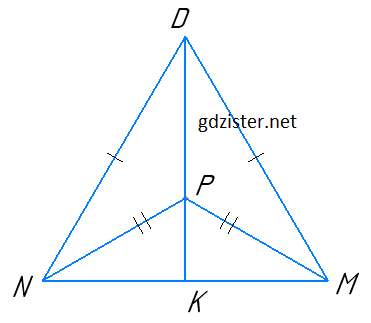
ΔDPN = ΔDPM за третьою ознакою рівності трикутників. Звідси виходить, що ∠MDP = ∠NDP, отже DK – бісектриса ΔDMN.
Оскільки у рівнобедреного трикутника бісектриса, що проведена до основи є також висотою і медіаною, то MK = KN.
