№ 410 Геометрія = № 31.12 Математика
Усередині рівнобедреного трикутника АВС (АВ = АС) взято точку К так, що ВК = КС. Доведіть, що пряма АК перпендикулярна до ВС.
Розв'язок:
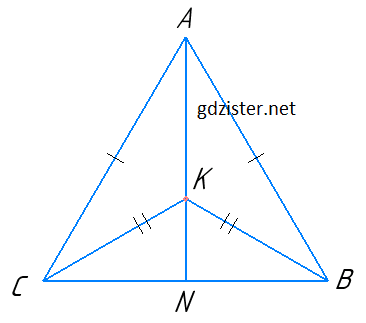
ΔACK = ΔABK за третьою ознакою рівності трикутників (оскільки AB = AC, BK = KC за умовою, AK — спільна сторона). ∠CAK = ∠BAK, оскільки у рівних трикутників відповідні кути рівні. Отже, AN — бісектриса трикутника ABC. У рівнобедреному трикутнику бісектриса, проведена до основи, є висотою, тобто AN ⊥ CB.
Оскільки K ∈ AN, то AK ⊥ CB.
