№ 386 Геометрія = № 30.15 Математика
Доведіть, що коли бісектриса трикутника є його висотою, то трикутник - рівнобедрений.
Розв'язок:
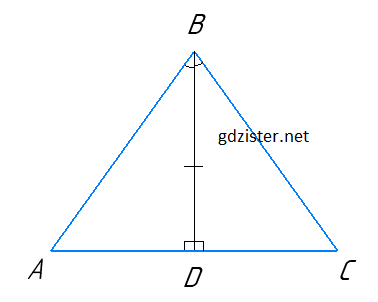
Нехай в ΔABC BD — бісектриса і висота.
∠ABD = ∠CBD, ∠BDA = ∠BDC, BD — спільна сторона ΔABD і ΔCBD.
Отже, ΔABD = ΔCBD за стороною і прилеглими кутами. Оскільки у рівних трикутників відповідні сторони рівні, то AB = CB. Отже, ΔABC — рівнобедрений.
