№ 357 Геометрія = № 29.14 Математика
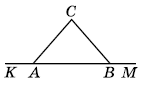
∆АВС - рівнобедрений з основою АВ. Доведіть, що ∠KAC = ∠MBC.
Розв'язок:
За умовою ΔABC — рівнобедрений, отже, AC = CB і ∠CAB = ∠CBA (за властивістю кутів рівнобедреного трикутника).
∠KAC і ∠CAB — суміжні,
∠KAC + ∠CAB = 180°,
∠KAC = 180° - ∠CAB.
∠MBC і ∠CBA — суміжні,
∠MBC + ∠CBA = 180°,
∠MBC = 180° - ∠CBA.
Оскільки ∠CAB = ∠CBA, то і ∠KAC = ∠MBC.
