№ 329 Геометрія = № 28.11 Математика
Дано: АО = ОС, ВО = OD.
Довести: АВ = CD, ВС = AD
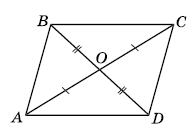
Розв'язок:
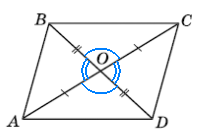
Розглянемо ΔBOC і ΔDOA: OC = OA, OB = OD, ∠BOC = ∠DOA, як вертикальні кути.
Отже, ΔBOC = ΔDOA за двома сторонами і кутом між ними.
Отже, BC = AD, оскільки у рівних трикутників відповідні сторони рівні.
Розглянемо ΔBOA і ΔDOC: AO = OC, OB = OD, ∠BOA = ∠DOC — як вертикальні кути.
Отже, ΔBOA = ΔDOC за двома сторонами і кутом між ними.
Отже, AB = CD, оскільки у рівних трикутників відповідні сторони рівні.
