№ 206 Геометрія = № 18.25 Математика
MF - бісектриса кута KMN, KF - бісектриса кута МКР. ∠MKF + ∠FMK = 90°. Доведіть, що MN ‖ КР.
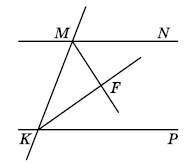
Розв'язок:
MF – бісектриса кута KMN, то ∠KMN = 2 ∙ ∠FMK;
KF – бісектриса кута MKP, то ∠MKP = 2 ∙ ∠MKF.
За умовою ∠MKF + ∠FMK = 90°.
Маємо ∠MKP + ∠KMN = 2 ∙ ∠MKF + 2 ∙ ∠FMK =
= 2(∠MKF + ∠FMK) = 2 ∙ 90° = 180°.
Кути MKP і KMN – внутрішні односторонні, утворені при перетині прямих MN і KP січною MK.
Оскільки ∠MKP + ∠KMN = 180°, то MN ∥ KP.
