№ 177 Геометрія = № 17.14 Математика
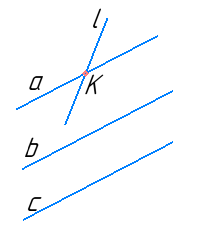
Прямі а і b - паралельні, прямі b і с також паралельні. Пряма l перетинає пряму а. Доведіть, що пряма l перетинає прямі b і с.
Розв'язок:
Припустимо, що пряма l не перетинає пряму b, тобто l ∥ b. Отже, через т. К проходять дві прямі l і а, і обидві паралельні прямій b. Це суперечить аксіомі про паралельність прямих. Отже, наше припущення є хибним, значить, правильним є те, що l перетинає пряму b.
За умовою b ∥ с. Ми довели, що пряма l перетинає пряму b. Аналогічно доводиться, що l пертинає с.