№ 196 Алгебра = № 3.38 Математика
Старовинна грецька задача. У Піфагора запитали: «Скільки учнів навчається у твоїй школі?». На що він відповів: «Половина всіх моїх учнів вивчає математику, чверть – музику, сьома частина мовчить, і, окрім того, є ще три жінки». Скільки учнів навчалося в школі Піфагора?
Розв'язок:
Позначимо загальну кількість учнів у школі Піфагора через N.
Відомо, що:
Половина учнів вивчає математику: $\frac{1}{2}$N
Чверть учнів вивчає музику: $\frac{1}{4}$N
Сьома частина учнів мовчить: $\frac{1}{7}$N
Окрім того, є ще три жінки: 3
Всі учні разом становлять:
$\frac{1}{2}$N + $\frac{1}{4}$N + $\frac{1}{7}$N + 3 = N
Щоб вирішити це рівняння, спочатку знайдемо спільний знаменник для дробів. Найменший спільний кратний для 2, 4 і 7 — це 28. Тому перетворимо дроби так, щоб у всіх був спільний знаменник:
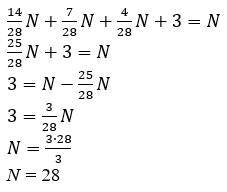
Отже, в школі Піфагора навчалося 28 учнів.
Відповідь:
28 учнів.
