Знайдіть гострі кути прямокутного трикутника, якщо зовнішні кути при вершинах цих кутів відносяться як 29 : 25.
Розв'язок:
Нехай у прямокутному трикутнику ABC (∠C = 90°) ∠A = x°, тоді ∠B = 90° − x°.
За властивістю суміжних кутів ∠PAB = 180° – x°, ∠RBA = 180° – (90° – x°) = 90° + x°.
За умовою задачі маємо:
$\frac{180° – x°}{29}$ = $\frac{90° + x°}{25}$, звідси 4500 – 25x = 2610 + 29x;
54x = 1890;
x = 35.
Отже, ∠A = 35°,
∠B = 90° – 35° = 55°.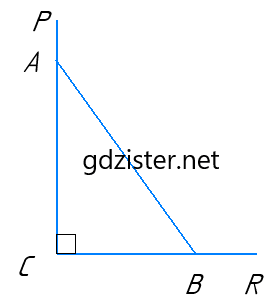
Відповідь:
35°, 55°.
