№ 577 Геометрія = № 2 ВПТ 8 Математика
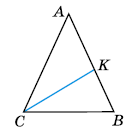
На малюнку CK — бісектриса рівнобедреного трикутника ABC з основою CB. Знайдіть:
1) ∠A, якщо ∠KCB = 32°;
2) ∠ACK, якщо ∠A = 56°.
Розв'язок:
1) Оскільки ∠KCB = 32° і СК – бісектриса, то ∠ACB = 2∠KCB = 2 · 32° = 64°.
∠B = ∠ACB = 64°, оскільки кути при основі рівнобедреного трикутника рівні.
Тоді ∠A = 180° – ∠ACB – ∠B = 180° – 64° – 64° = 52°.
2) ∠ACB = ∠B – оскільки ΔABC – рівнобедрений. ∠ACB = ∠B = $\frac{180° – 56°}{2}$ = 62°.
Оскільки СК – бісектриса, то ∠ACK = ∠KCB = $\frac{1}{2}$∠ACB = $\frac{1}{2}$ · 62° = 31°.
Відповідь:
1) 52°;
2) 31°.
