Завдання № 575

№ 575 Геометрія = № 32 ВПТ 6 Математика

Умова:

Доведіть рівність трикутників за двома сторонами та медіаною, проведеною до однієї з них.

Розв'язок:

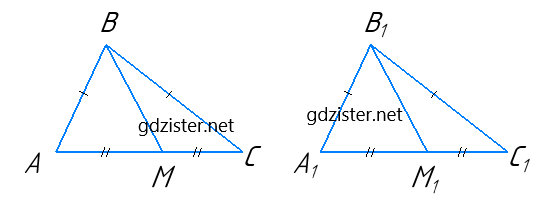
Нехай у трикутників △ABC і △A₁B₁C₁: AB = A₁B₁, AC = A₁C₁, BM = B₁M₁, де BM і B₁M₁ – медіани. Доведемо, що △ABC = △A₁B₁C₁. 

ΔABM = ΔA₁B₁M₁ – за трьома сторонами, оскільки AB = A₁B₁ – за умовою,
BM = B₁M₁ – за умовою, AM = A₁M₁ – як половини рівних сторін.

Із рівності трикутників маємо ∠A = ∠A₁. Тоді △ABC = △A₁B₁C₁ – за першою ознакою рівності трикутників, оскільки AB = A₁B₁ – за умовою, AC = A₁C₁ – за умовою, ∠A = ∠A₁ – за доведенням.

Відповідь: