№ 265 Геометрія = № 8 ВПТ 4 Математика
Доведіть, що коли бісектриси кутів АВС і CBD взаємно перпендикулярні, то точки А, В і D лежать на одній прямій.
Розв'язок:
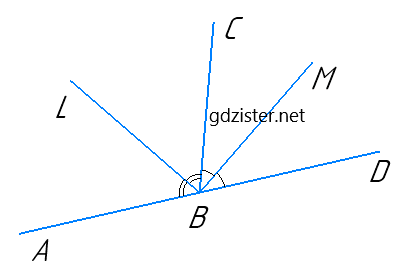
Нехай BL — бісектриса кута ABC. ∠ABC = 2∠LBC, BM — бісектриса кута CBD: ∠CBD = 2∠CBM.
Оскільки за умовою задачі бісектриси перпендикулярні, то ∠LBC + ∠CBM = 90°.
Знайдемо ∠ABD = ∠ABC + ∠CBD = 2∠LBC + 2∠CBM = 2(∠LBC + ∠CBM) = 2 × 90° = 180°.
Отже, кут ABD розгорнутий, точки A, B, D лежать на одній прямій.
