№ 262 Геометрія = № 5 ВПТ 4 Математика
На малюнку: АВ ⟂ CD, ∠KOC = ∠COL.
1) Чи правильно, що ∠AOK = ∠LOB, ∠AOL = ∠KOB?
2) Порівняйте ∠KOB і ∠AOK.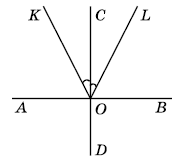
Розв'язок:
1) Оскільки AB ⊥ BC, то ∠AOC = 90°, ∠BOC = 90°.
∠AOK = ∠AOC − ∠KOC, ∠AOK = 90° − ∠KOC.
∠LOB = ∠BOC − ∠COL = 90° − ∠COL.
Оскільки ∠KOC = ∠COL, то ∠AOK = ∠LOB.
∠AOL = ∠AOC + ∠COL = 90° + ∠COL.
∠KOB = ∠COB + ∠KOC = 90° + ∠KOC.
Оскільки ∠KOC = ∠COL, то ∠AOL = ∠KOB.
2) ∠KOB = 90° + ∠KOC, ∠AOK = 90° − ∠KOC.
Отже, ∠AOK < ∠KOB.
