№ 461 Алгебра = № 20.33 Математика
Знайдіть усі натуральні значення n, для яких справджується нерівність $\frac{7}{12}$ < $\frac{n}{63}$ < $\frac{11}{18}$:
Розв'язок:
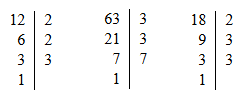
12 = 2 ∙ 2 ∙ 3; 63 = 3 ∙ 3 ∙ 7; 18 = 2 ∙ 3 ∙ 3.
НСК(12; 63; 18) = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 7 = 252.
$\frac{147}{252}$ < $\frac{4n}{252}$ < $\frac{154}{252}$;
4n = 148, 149, 150, 151, 152, 153.
n = 148 : 4 = 37
n = 150 : 4 = 37,5
n = 152 : 4 = 38
Відповідь:
n = 37, 38.
